Der Satz des Thales
Guten Tag, liebe Mathematiker! Heute haben wir ein ganz besonderes Highlight für euch – wir tauchen in die Welt der Kreise ein. Und ich verspreche, es wird nicht langweilig!
Bevor wir beginnen, lasst uns einen Moment innehalten und dem Mann applaudieren, der den heutigen Tag ermöglicht hat: Thales von Milet. Wer war das, fragt ihr? Nun, er war nur einer der coolsten Mathematiker der Antike. Ohne ihn wäre unsere Mathematik ein ganzes Stück weniger kreisförmig.
Jetzt aber genug der Vorrede, lasst uns direkt eintauchen!
Thales’ magischer Kreis
Thales hatte eine Obsession – Kreise. Aber er hatte auch eine Idee, die alles veränderte. Er sah einen Kreis und dachte sich: “Hmm, wenn ich einen Durchmesser zeichne und dann irgendeinen Punkt auf dem Kreisrand auswähle, um eine Dreiecksform zu machen… Oh, Moment mal… Ich glaube, das ist immer ein rechtwinkliges Dreieck!” Und so, meine Damen und Herren, wurde der Satz des Thales geboren.

Zack, Bumm, Rechter Winkel
Mit anderen Worten: Wählt man zwei beliebige Punkte auf einem Kreis, deren Verbindungsstrecke durch den Mittelpunkt des Kreises geht (auch Durchmesser genannt), und verbindet man einen dieser Punkte mit einem dritten Punkt auf dem Kreis, entsteht immer ein rechtwinkliges Dreieck. Immer. Egal, wo dieser dritte Punkt liegt. Es ist, als hätte Thales einen Zauberstab geschwungen und gesagt: “Zack, Bumm, rechter Winkel!”
Beispiel:
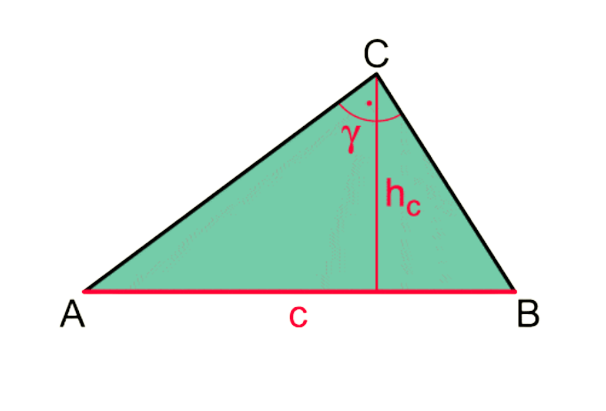
Von einem Dreieck sind c, h_c und γ=90° gegeben.
Konstruktionsbeschreibung:
Die Punkte A und B sind durch c festgelegt.
Der Punkt C liegt:
- auf dem Thaleskreis über
AB - auf einer Parallelen zu
ABim Abstandh_c.
Das Spiel mit den Tangenten
Nun, da wir den Satz des Thales gemeistert haben, springen wir zur nächsten Herausforderung: Tangenten. Was sind Tangenten, fragt ihr? Stellt euch vor, ihr seid auf einer Party (ja, eine Mathe-Party, ist das coolste, oder?) und es gibt diesen einen Typen, der nur kurz vorbeischaut und dann wieder geht. Dieser Typ ist wie eine Tangente – er berührt den Kreis an genau einem Punkt und geht dann seinen eigenen Weg.
Und Thales, der alte Schelm, hat uns auch hier einen Trick hinterlassen. Jede Tangente, die von einem Punkt auf dem Kreis gezogen wird, ist immer rechtwinklig zur Verbindungslinie vom Mittelpunkt des Kreises zu diesem Punkt. Es ist, als ob Thales die Tangentenparty crasht und sagt: “Hey, macht mal einen rechten Winkel!”
Beispiel: Tangenten an einen Kreis
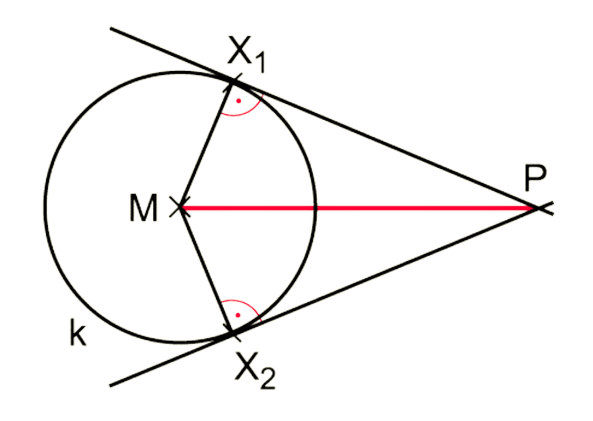
Es sollen die Tangenten an einen Kreis k durch einen Punkt P ausserhalb des Kreises konstruiert werden.
Vorbemerkungen:
Die gesuchten Berührungspunkte der Tangenten sind X1 und X2. Da Tangente und Berührungsradius senkrecht zueinander sind, gilt: ∢PX1M=90° bzw. ∢MX2P=90°.
Konstruktionsbeschreibung:
Der Punkt X liegt:
- auf dem Kreis
kund - auf dem Thaleskreis mit dem Durchmesser [PM].
Zusammenfassung
Also, um es kurz zu fassen: Thales hat uns zwei wichtige Dinge gelehrt. Erstens, wenn ihr jemals in einem Kreis verloren seid und einen Weg aus der Misere sucht, zieht einfach einen Durchmesser und einen Radius, und zack, ihr habt ein rechtwinkliges Dreieck. Zweitens, wenn ihr auf einer Kreisparty seid und ihr seht jemanden, der nur kurz vorbeischaut (die Tangente), dann ist das immer ein Zeichen für einen rechten Winkel.
Und das, liebe Freunde, ist der magische Kreis von Thales. Also, bis zur nächsten Mathe-Party!

Antworten