Einführung in die Trigonometrie
Hallo und herzlich willkommen zu Lektion 4! Schnall dich gut an, denn heute tauchen wir ein in die magische Welt der Trigonometrie! Und nein, “Trigonometrie” ist nicht der Name eines enttäuschenden Science-Fiction-Films, sondern etwas unendlich viel Spannenderes und Reales!
Trigonometrie, mein Freund, ist die Kunst der Dreiecke. Nicht irgendwelche Dreiecke, wie die, die du vielleicht früher aus Papier gefaltet hast. Nein, hier geht’s um mathematische Dreiecke! Schau dir ein rechtwinkliges Dreieck an – es gibt eine Menge an Informationen, die wir aus dieser einfachen Form gewinnen können, und das ist der Zauber der Trigonometrie.
Kommen wir zu den Hauptdarstellern unserer Show: Sinus, Kosinus und Tangens. Jeder hat seine eigene Rolle in unserem Trigonometrie-Drama und zusammen sind sie das Dreamteam der Dreiecksmathematik. Sie klingen vielleicht wie die Namen der neuesten Superhelden, aber in Wirklichkeit sind sie noch cooler! Warum? Weil sie uns helfen, selbst die kniffligsten Probleme mit Dreiecken, Winkeln und Abständen zu knacken!
- Sinus (kurz “sin”) ist ein Verhältnis, das uns die Beziehung zwischen der gegenüberliegenden Seite und der Hypotenuse in einem rechtwinkligen Dreieck zeigt.
- Kosinus (kurz “cos”) ist ein weiteres Verhältnis, das die Beziehung zwischen der anliegenden Seite und der Hypotenuse in einem rechtwinkligen Dreieck darstellt.
- Tangens (kurz “tan”) ist das dritte Verhältnis und der kleine Rebell der Gruppe. Er zeigt uns die Beziehung zwischen der gegenüberliegenden Seite und der anliegenden Seite in einem rechtwinkligen Dreieck.
Bisschen verwirrend? Keine Sorge, wir werden das alles Schritt für Schritt aufdröseln und du wirst dich fragen, warum du jemals Angst vor der Trigonometrie hattest!
Also, schnapp dir deinen Bleistift und dein Notizbuch und lass uns diese Trigonometrie-Reise starten! Bis zum Ende dieser Lektion wirst du verstehen und erklären können, wie Dreiecke, Winkel und Abstände mit Sinus, Kosinus und Tangens zusammenhängen. Klingt das nicht aufregend? Na dann, auf geht’s!
Schritt 1: Verstehe die Rollen von Sinus, Kosinus und Tangens
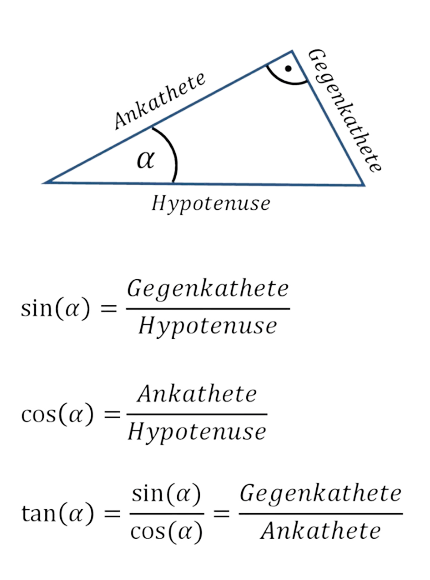
Lass uns das rechtwinklige Dreieck etwas genauer betrachten. Jedes rechtwinklige Dreieck hat eine Hypotenuse (die längste Seite gegenüber dem rechten Winkel), eine gegenüberliegende Seite und eine anliegende Seite.
Stell dir vor, das Dreieck ist eine Familie auf einem Familienfoto. Der Winkel, den du betrachtest, ist die Person, die das Foto aufnimmt. Die Hypotenuse ist wie der charmante Hund der Familie, der immer das Zentrum der Aufmerksamkeit ist, egal wo er ist. Die anliegende Seite steht neben dem Fotografen (wie ein geschwätziger Onkel) und die gegenüberliegende Seite steht gegenüber (wie die stille Tante, die immer in der Ecke sitzt).
Sinus, Kosinus und Tangens sind wie Filter auf dem Foto, die uns helfen, die Beziehungen zwischen den Familienmitgliedern besser zu verstehen.
- Sinus: Schau dir den Fotografen an und dann den Hund (die Hypotenuse). Sinus ist wie ein Filter, der dir zeigt, wie nahe der Hund (Hypotenuse) der stillen Tante (gegenüberliegende Seite) ist.
- Kosinus: Dieser Filter zeigt dir, wie nahe der Hund (Hypotenuse) dem geschwätzigen Onkel (anliegende Seite) ist.
- Tangens: Jetzt ignorieren wir den Hund (sorry, Hund!) und konzentrieren uns auf die stille Tante (gegenüberliegende Seite) und den geschwätzigen Onkel (anliegende Seite). Der Tangens-Filter zeigt uns ihr Verhältnis zueinander.
Schritt 2: Die Formeln von Sinus, Kosinus und Tangens

Jetzt wo du ihre Rollen verstehst, lassen Sie uns die mathematischen Formeln kennenlernen:
- sin(θ) = gegenüberliegende Seite / Hypotenuse
- cos(θ) = anliegende Seite / Hypotenuse
- tan(θ) = gegenüberliegende Seite / anliegende Seite
Denk daran, θ ist einfach der Winkel, den wir betrachten. θ könnte jeder sein, von Beyoncé bis zu deinem Klassenlehrer, und diese Formeln würden immer noch funktionieren!
Schritt 3: Anwenden der Trigonometrie
Jetzt wo du die Formeln kennst, lass uns sie ein bisschen ausprobieren. Nehmen wir an, wir haben ein rechtwinkliges Dreieck, und wir wissen, dass die Hypotenuse 10 Einheiten lang ist, und der Winkel θ ist 30 Grad. Wie können wir die Längen der anderen Seiten herausfinden?
Einfach! Mit unseren Superhelden: Sinus, Kosinus und Tangens!
Glaubst du mir nicht? Probier es aus und staune! Es ist als ob du einen Schlüssel zur Geheimwelt der Dreiecke hättest.
Aufgaben
Auf geht’s! Hier kommen zehn spannende Trigonometrie-Aufgaben, die dich herausfordern werden.
Aufgabe 1:
In einem rechtwinkligen Dreieck ist die Hypotenuse 10 cm lang und der Winkel gegenüber der Hypotenuse beträgt 30 Grad. Berechne die Länge der gegenüberliegenden Seite.
Aufgabe 2:
Ein rechtwinkliges Dreieck hat einen Winkel von 45 Grad und die anliegende Seite ist 7 cm lang. Wie lang ist die Hypotenuse?
Aufgabe 3:
In einem rechtwinkligen Dreieck beträgt die Länge der gegenüberliegenden Seite 5 cm und der Winkel ist 60 Grad. Berechne die Länge der Hypotenuse.
Aufgabe 4:
Ein Dreieck hat eine Hypotenuse von 20 cm und eine gegenüberliegende Seite von 10 cm. Berechne den Winkel.
Aufgabe 5:
Ein rechtwinkliges Dreieck hat eine anliegende Seite von 8 cm und einen Winkel von 30 Grad. Berechne die Länge der Hypotenuse.
Aufgabe 6:
Du stehst 15 Meter entfernt von einem Baum und der Winkel von deinem Standpunkt bis zur Spitze des Baumes beträgt 60 Grad. Wie hoch ist der Baum?
Aufgabe 7:
Ein Leuchtturm hat eine Höhe von 30 Meter. Wenn du 20 Meter entfernt stehst, unter welchem Winkel siehst du die Spitze des Leuchtturms?
Aufgabe 8:
Ein rechtwinkliges Dreieck hat eine Hypotenuse von 13 cm und eine gegenüberliegende Seite von 5 cm. Wie gross ist der Winkel?
Aufgabe 9:
Eine Leiter von 10 Metern Länge lehnt an einer Wand. Wenn die Leiter einen Winkel von 30 Grad zur Wand bildet, wie weit ist das untere Ende der Leiter von der Wand entfernt?
Aufgabe 10:
Ein rechtwinkliges Dreieck hat eine anliegende Seite von 6 cm und die Hypotenuse ist 10 cm lang. Wie groß ist der Winkel?
Denk daran, diese Aufgaben können mit den Trigonometrie-Formeln gelöst werden, die wir oben gelernt haben. Viel Spass beim Knacken dieser Aufgaben!
Lösungen
Hier sind die Lösungen für die gegebenen Aufgaben:
Aufgabe 1:
Du kannst den Sinus verwenden, um die Länge der gegenüberliegenden Seite zu berechnen. Sinus von 30 Grad ist 0,5.
Sin(30) = Gegenüberliegende Seite / Hypotenuse
0.5 = Gegenüberliegende Seite / 10
Gegenüberliegende Seite = 0.5 * 10 = 5 cm
Aufgabe 2:
Hier können wir den Kosinus verwenden, da wir die anliegende Seite kennen.
Kosinus von 45 Grad ist etwa 0.7071.
Kos(45) = Anliegende Seite / Hypotenuse
0.7071 = 7 / Hypotenuse
Hypotenuse = 7 / 0.7071 = 9.9 cm
Aufgabe 3:
In diesem Fall benutzen wir den Sinus.
Sin(60) = Gegenüberliegende Seite / Hypotenuse
0.8660 = 5 / Hypotenuse
Hypotenuse = 5 / 0.8660 = 5.77 cm
Aufgabe 4:
Wir müssen hier den Sinus-Wert verwenden, um den Winkel zu finden.
Sin(Winkel) = Gegenüberliegende Seite / Hypotenuse
Sin(Winkel) = 10 / 20 = 0.5
Der Winkel ist Sinus inverse von 0.5, das ist 30 Grad
Aufgabe 5:
Wir verwenden den Kosinus.
Kos(30) = Anliegende Seite / Hypotenuse
0.8660 = 8 / Hypotenuse
Hypotenuse = 8 / 0.8660 = 9.24 cm
Aufgabe 6:
Wir verwenden den Tangens.
Tan(60) = Baumhöhe / Entfernung
1.7321 = Baumhöhe / 15
Baumhöhe = 1.7321 * 15 = 25.98 Meter
Aufgabe 7:
Wir können den Tangens verwenden, um den Winkel zu berechnen.
Tan(Winkel) = Höhe / Entfernung
Tan(Winkel) = 30 / 20 = 1.5
Der Winkel ist Tangens inverse von 1.5, das ist 56.31 Grad
Aufgabe 8:
Wir verwenden den Sinus, um den Winkel zu berechnen.
Sin(Winkel) = Gegenüberliegende Seite / Hypotenuse
Sin(Winkel) = 5 / 13 = 0.3846
Der Winkel ist Sinus inverse von 0.3846, das ist 22.62 Grad
Aufgabe 9:
Wir verwenden den Kosinus, um die Entfernung zur Wand zu berechnen.
Kos(30) = Entfernung / Leiterlänge
0.8660 = Entfernung / 10
Entfernung = 0.8660 * 10 = 8.66 Meter
Aufgabe 10:
Wir verwenden den Kosinus, um den Winkel zu berechnen.
Kos(Winkel) = Anliegende Seite / Hypotenuse
Kos(Winkel) = 6 / 10 = 0.6
Der Winkel ist Kosinus inverse von 0.6, das ist 53.13 Grad
Das ist alles für heute. Morgen werden wir weiter in die Tiefe der Trigonometrie tauchen. Bring deinen Taucheranzug mit! Bis dahin – keep it triggy!

Antworten