Einführung in Funktionen und Graphen

Hey ihr alle! In dieser Lektion werden wir in die faszinierende Welt der Funktionen und Graphen eintauchen. Funktionen sind wie magische Maschinen, die uns helfen, Zusammenhänge zwischen verschiedenen Dingen zu verstehen. Stellt euch vor, ihr habt eine Funktion, die euch sagt, wie viel Geld ihr für eine bestimmte Anzahl von Arbeitsstunden verdient. Das wäre doch toll, oder?

Was ist eine Funktion

Eine Funktion ist im Grunde genommen eine Regel, die eine Eingabe in eine Ausgabe umwandelt. Nehmen wir an, ihr gebt einer Funktion euer Alter als Eingabe, und die Funktion gibt euch eure Körpergrösse als Ausgabe. Das ist eine ziemlich coole Funktion, oder?

Darstellung von Funktionen durch Graphen

Aber wie stellen wir eine Funktion grafisch dar? Das ist der Moment, in dem Graphen ins Spiel kommen. Ein Graph ist wie eine visuelle Darstellung einer Funktion. Es ist wie eine Landkarte, die uns zeigt, wie sich die Werte verändern.

Verständnis der x- und y-Achse in einem Graphen

Auf einem Graphen haben wir normalerweise eine x-Achse und eine y-Achse. Die x-Achse repräsentiert die Eingabewerte, während die y-Achse die Ausgabewerte darstellt. Stellt euch vor, wir haben eine Funktion, die den Verlauf der Temperatur über den Tag hinweg beschreibt. Auf der x-Achse haben wir die Uhrzeit und auf der y-Achse haben wir die Temperatur. So können wir leicht erkennen, wie sich die Temperatur im Laufe des Tages ändert.

Achsenabschnitte und Steigungen

Was ist mit Achsenabschnitten und Steigungen? Achsenabschnitte sind die Punkte, an denen der Graph die Achsen schneidet. Sie geben uns wichtige Informationen über den Startpunkt und den Nullpunkt des Graphen. Steigungen hingegen zeigen uns, wie schnell sich der Graph verändert. Je steiler der Graph ansteigt, desto grösser ist die Steigung.

Anwendung von Funktionen auf praktische Beispiele

Jetzt kommt der aufregende Teil: Anwendung von Funktionen auf praktische Beispiele! Funktionen können uns helfen, verschiedene Alltagsprobleme zu lösen. Nehmen wir an, ihr möchtet wissen, wie viel Geld ihr für eine bestimmte Anzahl von Stunden Arbeit verdient. Hier kommt eine lineare Funktion ins Spiel. Sie hat eine gerade Linie als Graphen und zeigt uns den Zusammenhang zwischen Arbeitsstunden und Verdienst.

Beschreibung
Die Funktion y = 15x ist eine lineare Funktion, die den Zusammenhang zwischen Arbeitsstunden (x) und Verdienst (y) darstellt.

Jede lineare Funktion hat die Form y = mx + b, wobei m die Steigung der Linie und b der y-Achsenabschnitt ist. In dieser speziellen Funktion ist m gleich 15, was bedeutet, dass für jede zusätzliche Arbeitsstunde der Verdienst um 15 CHF steigt. Das ist die Steigung der Linie. Da b nicht in der Funktion angegeben ist, ist es gleich 0, was bedeutet, dass die Linie die y-Achse beim Ursprung (0,0) schneidet.

Das bedeutet konkret: Wenn man 0 Stunden arbeitet, verdient man 0 Euro. Wenn man 1 Stunde arbeitet, verdient man 15 CHF. Wenn man 2 Stunden arbeitet, verdient man 30 CHF. Und so weiter. Jede zusätzliche Arbeitsstunde führt zu einem zusätzlichen Verdienst von 15 CHF.

Zusammengefasst: Die Funktion y = 15x stellt einen direkten, linearen Zusammenhang zwischen Arbeitsstunden und Verdienst dar, wobei jeder Arbeitsstunde 15 CHF Verdienst entspricht.

Um den Graphen einer linearen Funktion zu zeichnen, benötigen wir nur zwei Punkte. Mit diesen beiden Punkten können wir die Linie erstellen und den Zusammenhang erkennen. Wenn wir weitere Punkte hinzufügen, können wir den Verlauf der Funktion besser verstehen.

In den Übungen werden wir praktische Beispiele bearbeiten und die Graphen von Funktionen erstellen. Ihr werdet sehen, wie Funktionen und Graphen uns helfen können, die Welt um uns herum besser zu verstehen. Also lasst uns loslegen und die Magie der Funktionen und Graphen entdecken!

Viel Spass und bis zur nächsten Lektion!

Übungen

1. Betrachte die folgende Funktion: f(x) = 2x + 3. Zeichne den Graphen dieser Funktion im Koordinatensystem. Bestimme den Achsenabschnitt und die Steigung des Graphen.
2. Gegeben ist die Funktion g(x) = 5 - x. Zeichne den Graphen dieser Funktion und finde den Achsenabschnitt und die Steigung.
3. Eine Funktion h(x) hat den Graphen einer horizontalen Linie. Zeichne den Graphen und gib den Funktionswert für h(4) an.
4. Die Funktion k(x) = -0,5x + 2 hat den Graphen einer Geraden. Zeichne den Graphen und finde den Achsenabschnitt und die Steigung.
5. Betrachte die Funktion f(x) = x^2. Zeichne den Graphen dieser Funktion und bestimme den Funktionswert für f(3).
6. Die Funktion g(x) = 4x - 1 hat den Graphen einer Geraden. Zeichne den Graphen und finde den Achsenabschnitt und die Steigung.
7. Gegeben ist die Funktion h(x) = -3. Zeichne den Graphen dieser Funktion, der eine horizontale Linie ist.
8. Die Funktion k(x) = 2x^2 - 5 hat den Graphen einer Parabel. Zeichne den Graphen und finde den Scheitelpunkt der Parabel.
9. Betrachte die Funktion f(x) = 3x + 2. Zeichne den Graphen dieser Funktion und bestimme den Funktionswert für f(0).
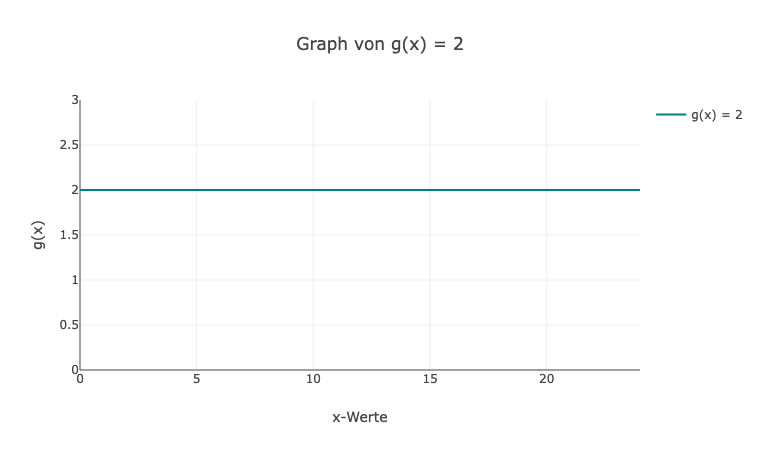
10. Die Funktion g(x) = 2 hat den Graphen einer horizontalen Linie. Zeichne den Graphen und gib den Funktionswert für g(7) an.

Lösungen

1. Der Graph von f(x) = 2x + 3 ist eine Gerade. Der Achsenabschnitt ist bei (0, 3) und die Steigung beträgt 2.

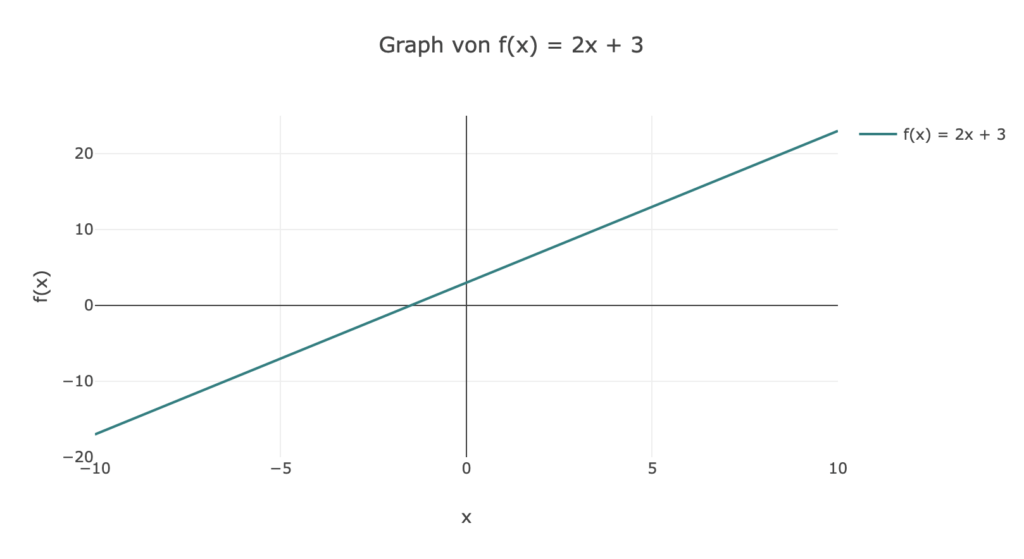
2. Der Graph von g(x) = 5 - x ist ebenfalls eine Gerade. Der Achsenabschnitt ist bei (0, 5) und die Steigung beträgt -1.

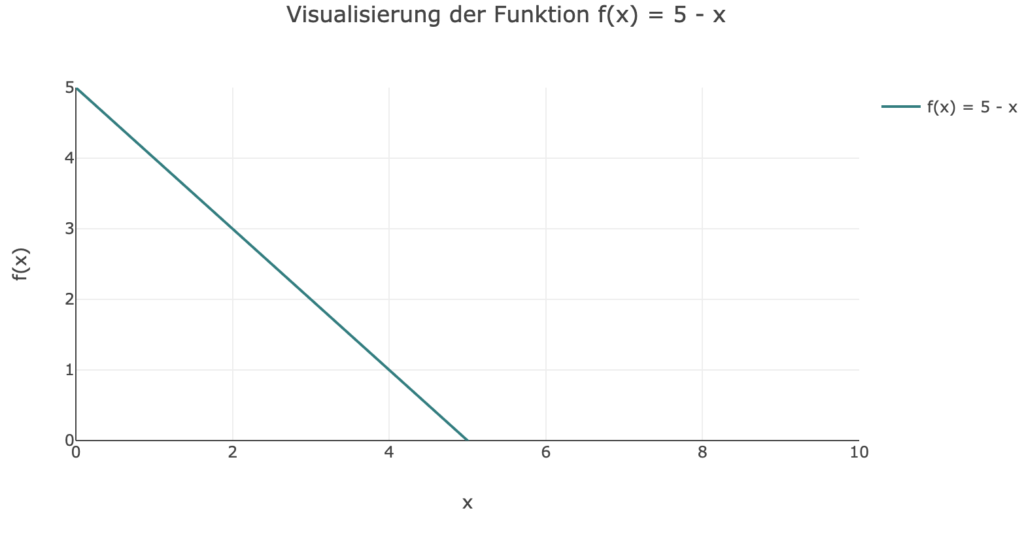
3. Da die Funktion h(x) eine horizontale Linie ist, ist der Graph eine gerade, waagerechte Linie. Der Funktionswert für h(4) ist immer gleich und wird mit h(4) = -3 angegeben.

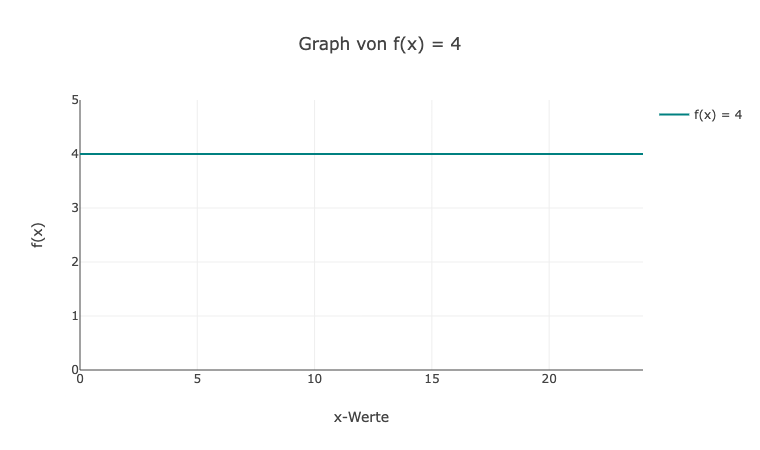
4. Der Graph von k(x) = -0,5x + 2 ist eine Gerade. Der Achsenabschnitt ist bei (0, 2) und die Steigung beträgt -0,5.

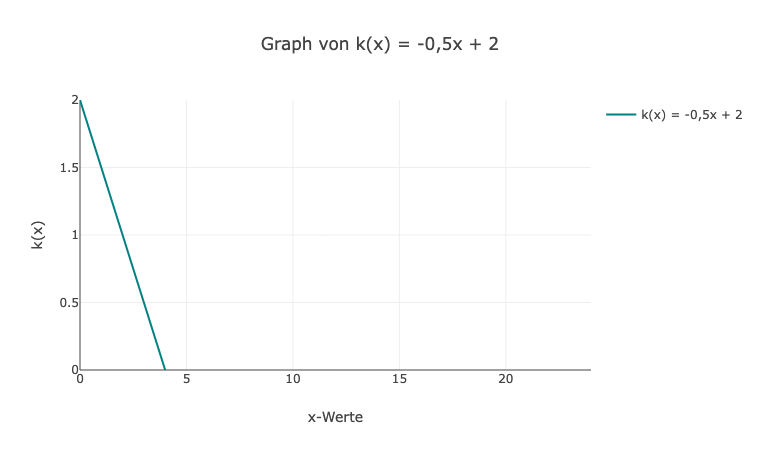
5. Der Graph von f(x) = x^2 ist eine nach oben geöffnete Parabel. Um den Funktionswert für f(3) zu berechnen, setzen wir x = 3 in die Funktion ein: f(3) = (3)^2 = 9.

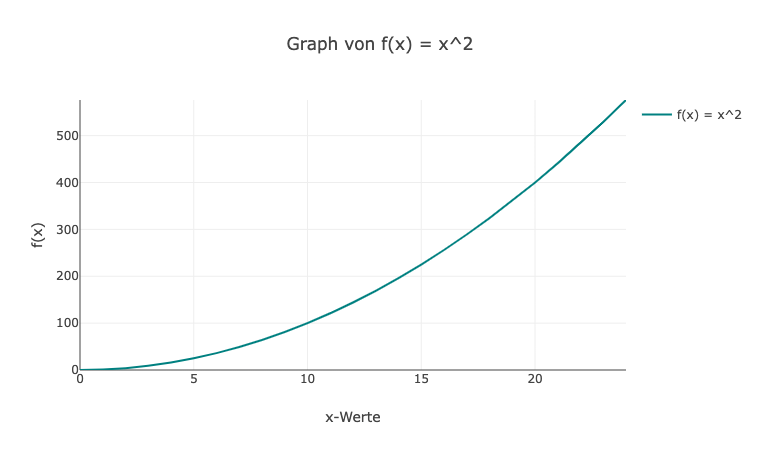
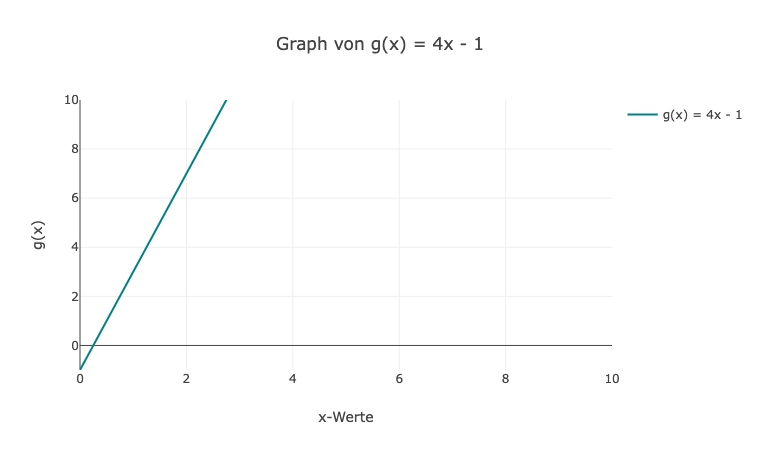
6. Der Graph von g(x) = 4x - 1 ist eine Gerade. Der Achsenabschnitt ist bei (0, -1) und die Steigung beträgt 4.

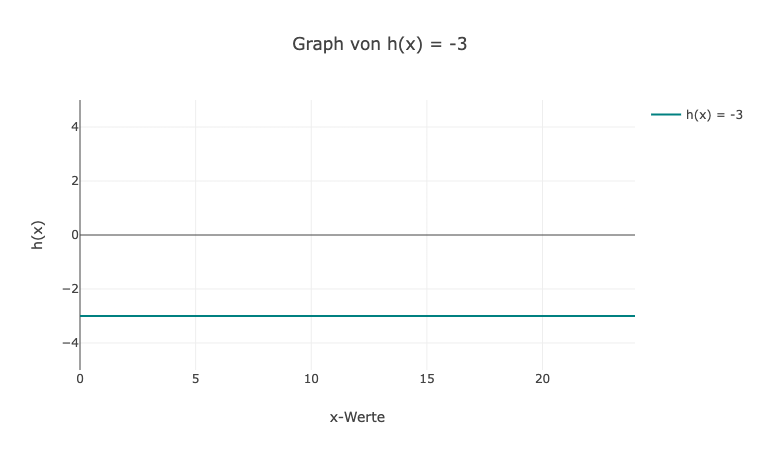
7. Da die Funktion h(x) eine horizontale Linie ist, ist der Graph eine gerade, waagerechte Linie. Der Funktionswert für jeden x-Wert ist immer gleich und wird mit h(x) = -3 angegeben.

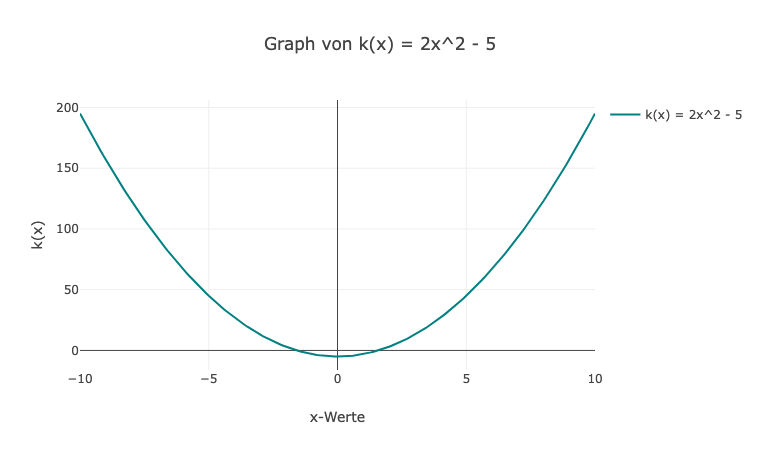
8. Der Graph von k(x) = 2x^2 - 5 ist eine nach oben geöffnete Parabel. Um den Scheitelpunkt der Parabel zu finden, verwenden wir die Formel x = -b / (2a) für quadratische Funktionen in der Form ax^2 + bx + c. Hier ist a = 2 und b = 0, also ist der Scheitelpunkt bei x = 0. Um den Funktionswert an diesem Punkt zu finden, setzen wir x = 0 in die Funktion ein: k(0) = 2(0)^2 - 5 = -5.

9. Der Graph von f(x) = 3x + 2 ist eine Gerade. Der Achsenabschnitt ist bei (0, 2) und die Steigung beträgt 3. Der Funktionswert für f(0) ist f(0) = 3(0) + 2 = 2.

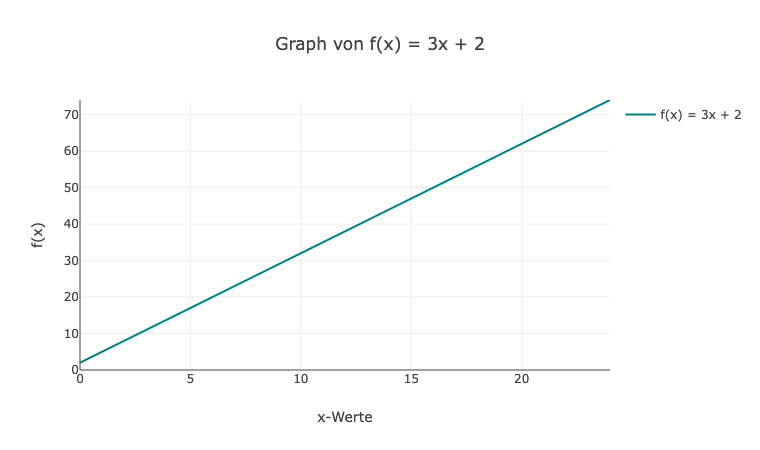
10. Da die Funktion g(x) eine horizontale Linie ist, ist der Graph eine gerade, waagerechte Linie. Der Funktionswert für jeden x-Wert ist immer gleich und wird mit g(x) = 2 angegeben. Daher ist der Funktionswert für g(7) gleich g(7) = 2.