Lineare Funktionen und ihre Graphen

Hallo zusammen, willkommen zu Lektion 5: “Lineare Funktionen und ihre Graphen”. Bevor wir loslegen, stellen wir uns vor, wir seien im Aufzug eines großen Gebäudes. Jeder Stock, den der Aufzug hochfährt, ist wie eine Stufe auf der y-Achse unseres Koordinatensystems. Der Weg, den der Aufzug zurücklegt, ist gerade und stetig, genau wie eine lineare Funktion.

Eigenschaften und Darstellung von linearen Funktionen

Du kennst schon die x- und y-Achse auf einem Graphen, richtig? Eine lineare Funktion ist eine gerade Linie auf diesem Graphen. Sie hat eine konstante Steigung, das bedeutet, sie steigt (oder fällt) gleichmässig. Du kannst sie mit der Formel y = mx + b darstellen, wobei m die Steigung der Linie ist und b der y-Achsenabschnitt, also der Punkt, an dem die Linie die y-Achse kreuzt.

Interpretation von Steigung und y-Achsenabschnitt in linearen Funktionen

Die Steigung m ist wie die Geschwindigkeit unseres Aufzugs. Eine hohe Steigung bedeutet, dass der Aufzug schnell fährt. Eine negative Steigung hingegen bedeutet, dass der Aufzug nach unten fährt. Der y-Achsenabschnitt b ist der Stock, auf dem der Aufzug startet, bevor er seine Fahrt beginnt.

Übungen zur Identifizierung, Zeichnung und Interpretation von linearen Funktionen

Jetzt ist es Zeit für dich, ein Aufzugsführer zu werden! Ich gebe dir ein paar lineare Funktionen, und deine Aufgabe ist es, diese Funktionen in einem Koordinatensystem zu zeichnen. Versuche, die Steigung und den y-Achsenabschnitt jeder Funktion zu interpretieren. Was bedeutet das für unseren Aufzug? Auf welchem Stock startet er und wie schnell oder langsam fährt er?

Hier kannst du die Graphen zeichnen. Setze deine Wunschwerte für a und b der Formel ein:

y = ax + b

a: b: Zeichnen

Übungen

Übung 1: Zeichne die folgenden linearen Funktionen in ein Koordinatensystem und markiere den y-Achsenabschnitt (b):

1. y = 2x + 1
2. y = -3x + 2
3. y = 0.5x - 1

Übung 2: Jetzt gehen wir in die andere Richtung. Sieh dir die folgenden Graphen an und bestimme die Gleichung der dargestellten linearen Funktion (Hinweis: Du musst die Steigung (m) und den y-Achsenabschnitt (b) herausfinden):

1. Ein gerader Graph startet bei y = 1 und fällt um 2 Einheiten auf der y-Achse für jede Einheit auf der x-Achse.
2. Ein gerader Graph startet bei y = -1 und steigt um 3 Einheiten auf der y-Achse für jede Einheit auf der x-Achse.
3. Ein gerader Graph startet bei y = 0 und bleibt konstant, unabhängig von der Position auf der x-Achse.

Übung 3: Interpretiere die folgenden linearen Funktionen im Zusammenhang mit unserem Aufzug-Beispiel:

1. y = 4x + 3
2. y = -2x + 5
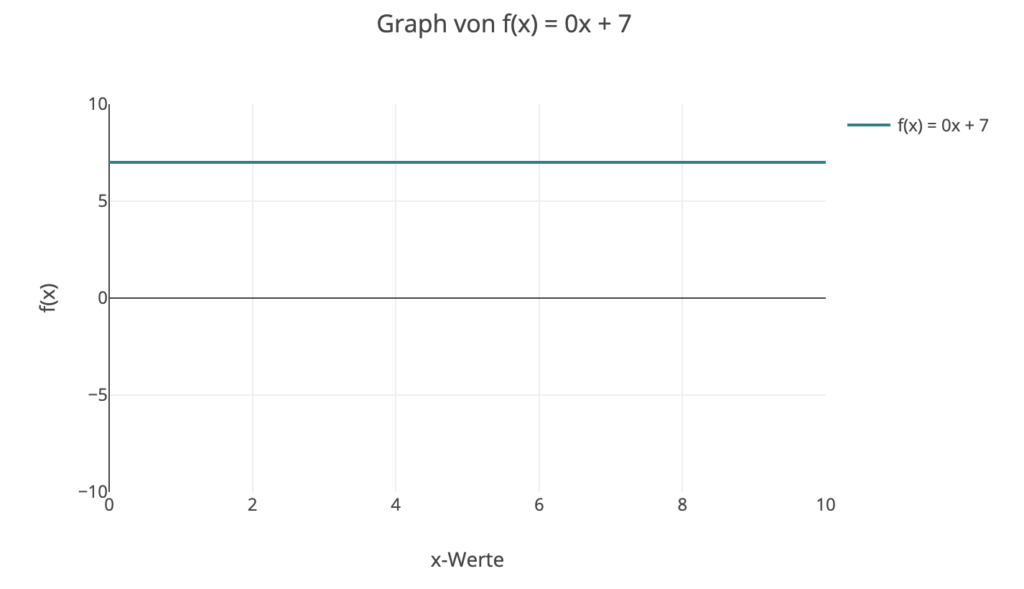
3. y = 0x + 7

Denke daran, dass die Steigung (m) die Geschwindigkeit des Aufzugs repräsentiert und der y-Achsenabschnitt (b) den Startstock darstellt. Wie schnell und in welche Richtung bewegt sich der Aufzug? Wo startet er?

Lösungen

Lösung Übung 1: Bei diesen Aufgaben musstest du lineare Funktionen in ein Koordinatensystem zeichnen und den y-Achsenabschnitt (b) markieren.

1. Bei der Funktion y = 2x + 1 hat der Graph eine positive Steigung von 2 und kreuzt die y-Achse bei y = 1.

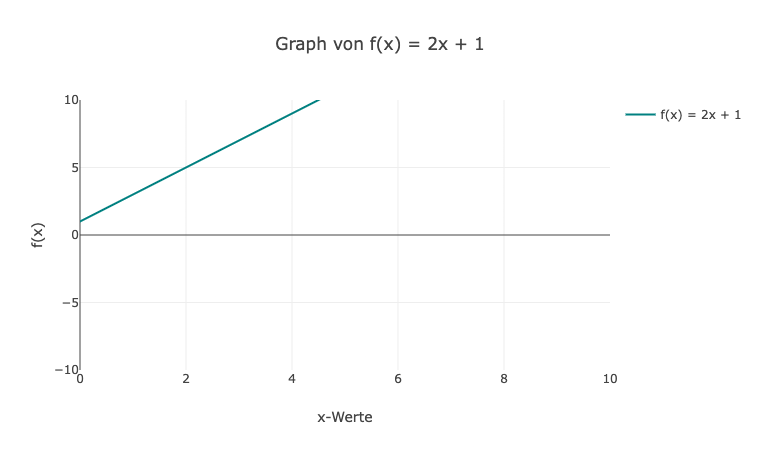
2. Der Graph von y = -3x + 2 fällt mit einer Steigung von -3 und kreuzt die y-Achse bei y = 2.

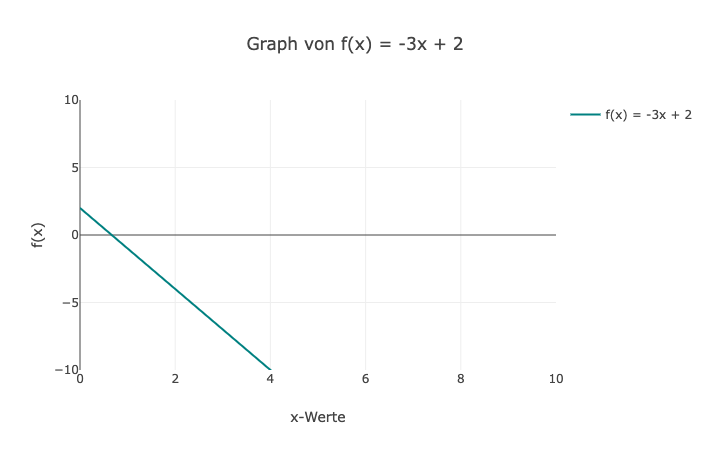
3. Bei y = 0.5x - 1 hat der Graph eine positive Steigung von 0.5 und kreuzt die y-Achse bei y = -1.

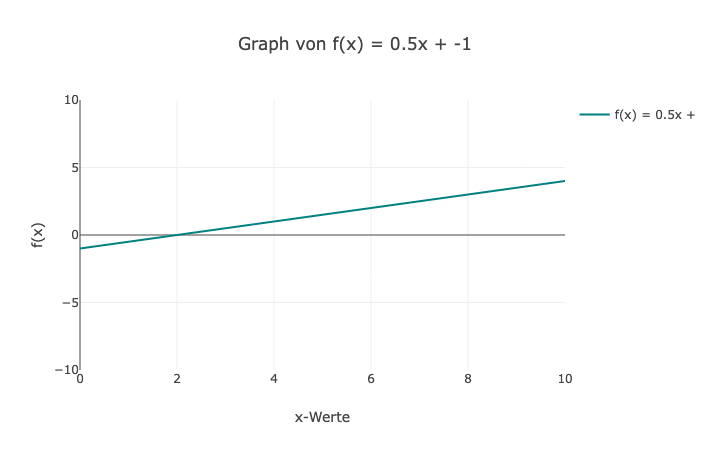
Lösung Übung 2: Hier musstest du die Gleichung der dargestellten linearen Funktion bestimmen:

1. Der Graph startet bei y = 1 und fällt um 2 Einheiten auf der y-Achse für jede Einheit auf der x-Achse. Die Gleichung ist y = -2x + 1.

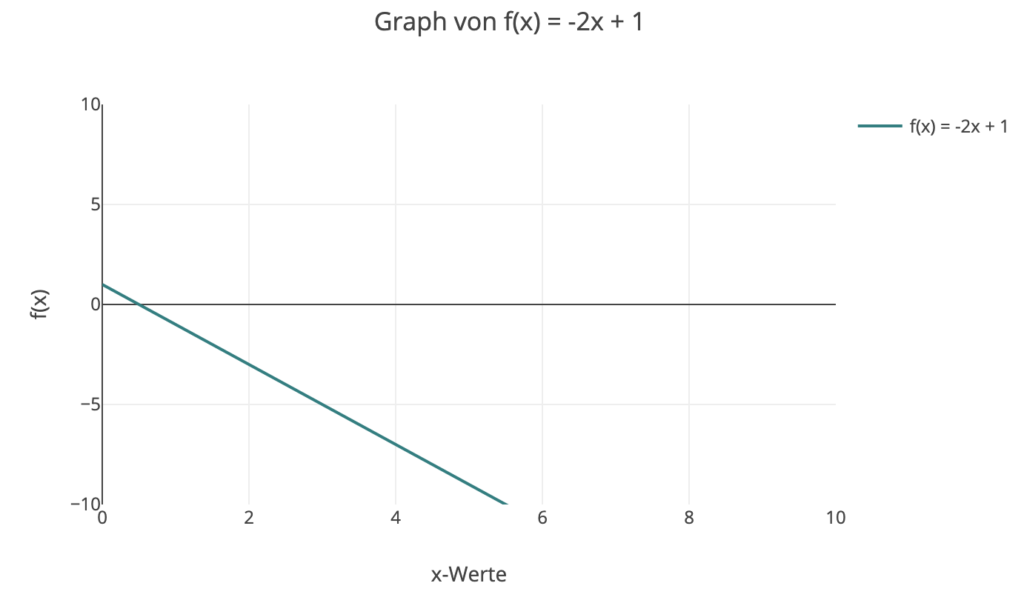
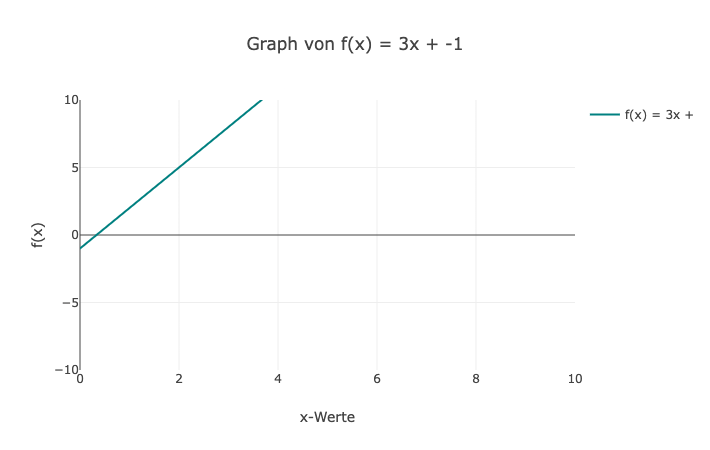
2. Der Graph startet bei y = -1 und steigt um 3 Einheiten auf der y-Achse für jede Einheit auf der x-Achse. Die Gleichung ist y = 3x - 1.

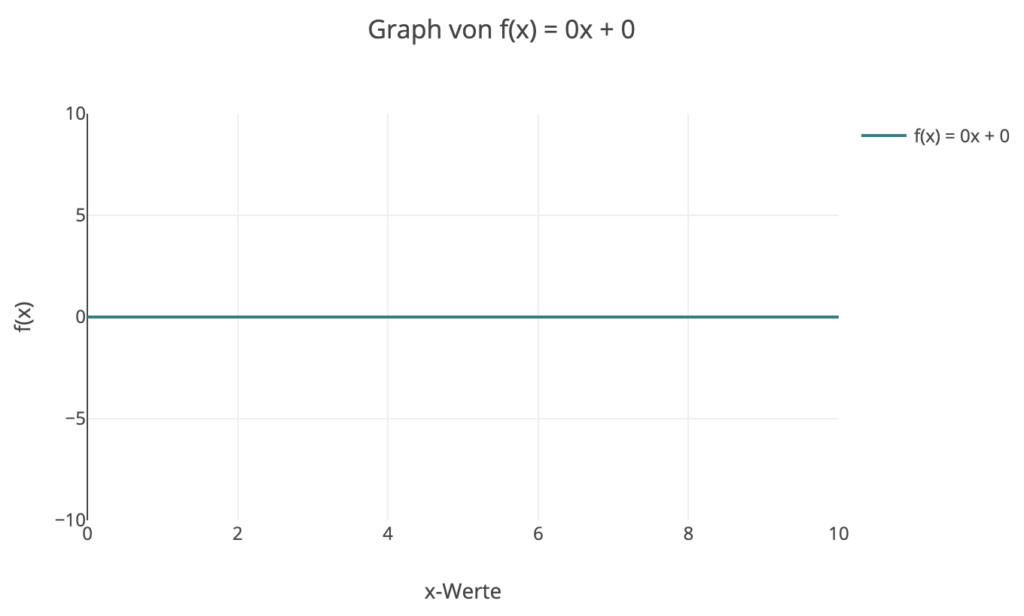
3. Der Graph startet bei y = 0 und bleibt konstant, unabhängig von der Position auf der x-Achse. Da die Linie horizontal verläuft, ist die Steigung 0, daher ist die Gleichung y = 0x oder einfach y = 0.

Lösung Übung 3: Hier musstest du die linearen Funktionen im Kontext unseres Aufzug-Beispiels interpretieren:

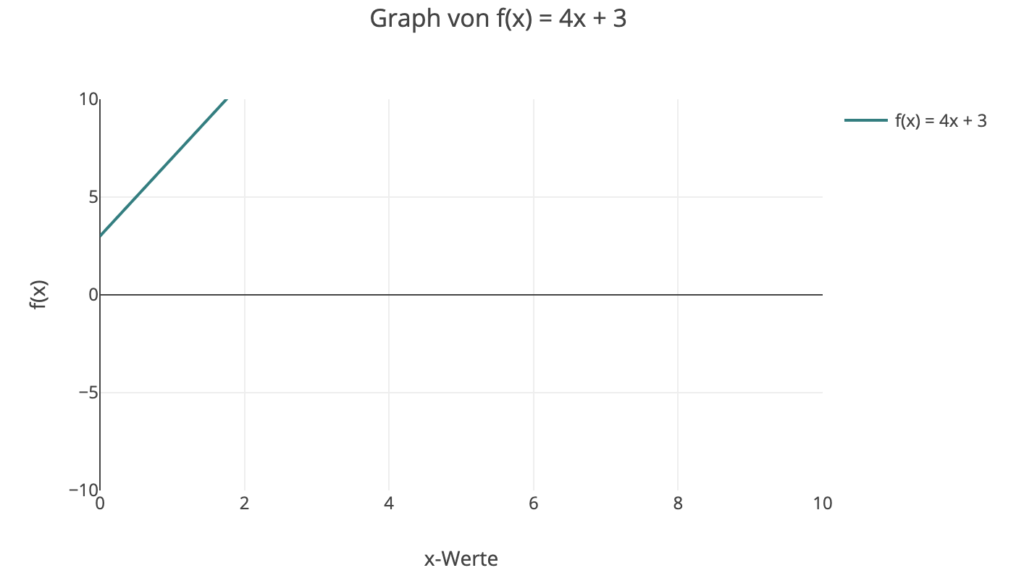
1. Bei y = 4x + 3 startet der Aufzug auf dem 3. Stock und fährt mit einer Geschwindigkeit von 4 Stockwerken pro Zeitseinheit nach oben.

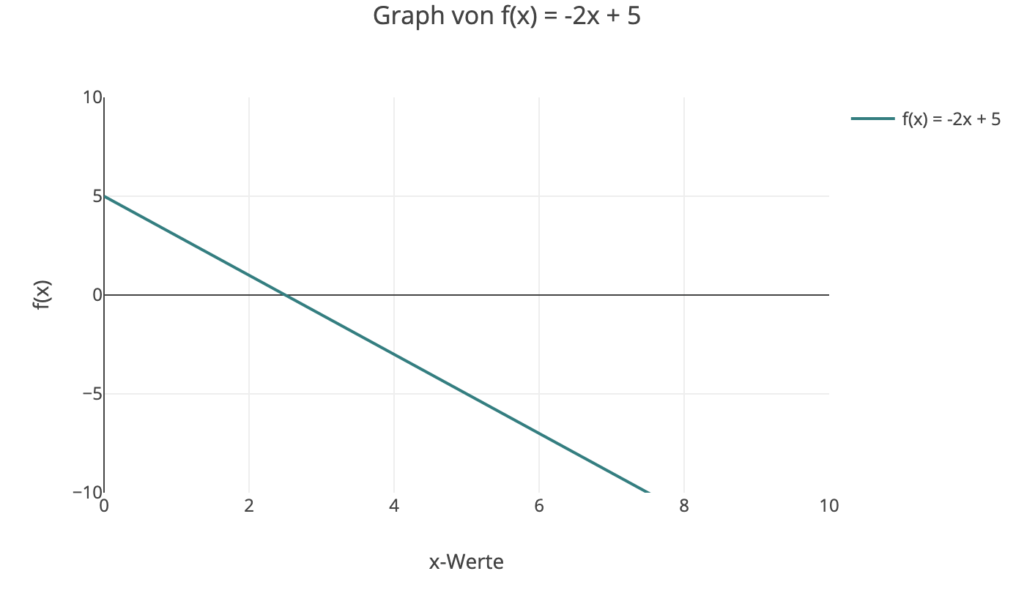
2. Bei y = -2x + 5 startet der Aufzug auf dem 5. Stock und fährt mit einer Geschwindigkeit von 2 Stockwerken pro Zeitseinheit nach unten.

3. Bei y = 0x + 7 bleibt der Aufzug auf dem 7. Stock stehen, egal wie viel Zeit vergeht, da die Geschwindigkeit (Steigung) 0 ist.

Das war's für heute. Denk dran, das Lernen von Mathematik ist wie das Fahren eines Aufzugs. Manchmal geht es rauf, manchmal runter, aber mit jeder Fahrt verstehst du ein bisschen mehr. Bis zum nächsten Mal!